Dr. Masaru Onoda, a researcher of the Correlated Electron Research Center (CERC), National Institute of Advanced Industrial Science and Technology (AIST), an independent administrative institution, studied the effect of polarization to the propagation of light wave packet and derived a new basic equations of geometrical optics taking this effect into consideration, in collaboration with Dr. Shuichi Murakami and Prof. Naoto Nagaosa, of the Faculty of Engineering (FOE), University of Tokyo (UOT), another independent administrative institution. These equations predict that the polarization affects the trajectory of light beam and causes a shift of the beam in the direction perpendicular to change of dielectric constant. This phenomenon is designated “optical Hall effect”. This means that the law of light reflection and refraction (Snell’s law), appearing in primary school textbooks, is to be rewritten. It is a discovery of great significance in physics. The effect, not predicted from the conventional geometrical optics, is closely linked with the law of total angular momentum conservation of photon, and also related with the fundamental principle of optical communications and quantum computer based on the degree of freedom of photon spin. The research group of CERC-AIST and FOE-UOT has proposed to amplify the effect extensively by use of photonic crystal, and is going to pursue the possibility of bringing about a breakthrough in these areas. The study has been carried out under the contract, cooperation and support from the Japan Science and Technology Agency (JST), another independent administrative institution.

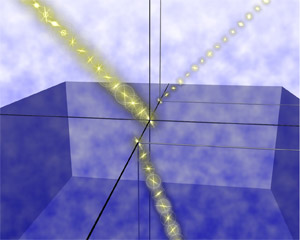
Fig. 1. Reflection and refraction of light at an interface between two media of different refractive indices. When the incident light is circularly polarized, the mid-axes of reflected and refracted light beams pass through a plane different from the trajectory of incident light.

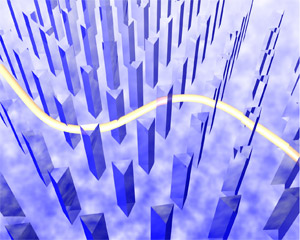
Fig. 2. When a slow spatial change in dielectric constant is applied to a 2-dimensional photonic crystal, the light beam is shifted in a direction perpendicular to the change.

The result was published in the August 20 issue of the Physical Review Letters, cited in the July 22nd issue of the on-line Physics New Update of the American Institute of Physics (AIP), as well as in the News and Views of the Nature.

The relationship of geometrical optics to wave optics resembles that of classical mechanics to quantum mechanics, and is regarded to be a matter of fundamental significance for physics. Nevertheless, many of physicists consider it an issue of the past already having been solved. For taking wave characteristics into geometrical optics, “diffraction theory” has been used, but in this process, the degree of freedom for polarization has been ignored. In this study, equations of geometrical optics fully describing the effect of polarization are derived, leading to cover a new phenomenon, optical Hall effect. In view of technology, the study on light propagation involves essential problems in areas of optical communications and quantum computer based on photonics. The present work is expected to provide a theoretical foundation for developing optical devices using photonic crystals.

The Strong Correlation Theory Team of the CERC-AIST is dedicated to the exploitation of functions of electron in solid without energy loss, paying attention to the key role of geometrical effect in the wave phenomena of electron. In particular, emphasis has been placed on the theoretical investigation for new phenomena based on geometrical phase (Berry phase) related to internal degree of freedom for “rotation” or spin, shared by electron and light. In fiscal year 2003, field-induced spin flux was proposed as a counterpart of electron spin in the semiconductor. [Science 301, 5638, 1348-1351] In the course of seeking the counterpart of the new effect based on Berry phase in optics, the “optical Hall effect” was discovered.

The behavior of light can be fully understood in principle by solving Maxwell’s equation for electromagnetism, but its analysis requires very complicated process. In geometrical optics, it has been shown that the trajectory of light of extremely short wavelength can be handled as a particle, making it possible to design and develop a number of optical instruments. However, when the dielectric constant changes in a spatial scale as large as wavelength, corrections from geometrical optics is needed in photonic crystals, for instance, and it is urgently needed to build up “extended geometric optics” to cover the latter case. So far, this problem has been handled by the “diffraction theory”, where the polarization has not been taken into consideration. In this study, new equation of geometrical optics has been derived successfully to extend the realm of geometrical optics. By using this equation, it has been demonstrated that a new phenomenon, “optical Hall effect”, i.e., shifting the trajectory of light beam in the direction perpendicular to change in dielectric constant can be fully clarified. This means that the law of light reflection and refraction at an interface between two media of different refractive indices, or Snell’s law, has to be modified. In this case, the magnitude of trajectory shift is as small as a fraction of wavelength, and has been left unnoticed. However, when a photonic crystal is used, the optical Hall effect is greatly amplified, to be useful and significant for the development of micro-machined optical devices.

This study has been carried out under a research theme “Coherence Control of Correlated Electron” in the research domain “Control and Utilization of Nano-Structures and Materials toward Realization of Advanced Information Processing and Communications” of the Strategic Creative Research Promotion Program (CREST-type Research) of the JST.

Let us consider a case of reflection and refraction of light at an interface between two media of different refractive indices, for the purpose of illustrating the difference between the conventional geometrical optics and the optics taking polarization or spin into consideration. A light beam traveling through the upper medium and falling to the interface at a certain angle is refracted to enter the lower medium. A reflected beam is also shown in the figure.

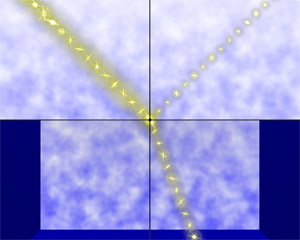
Fig. 3.

 

The refracting angle specified by Snell’s law is identical for two cases with and without degree of freedom for polarization (spin). According to the conventional geometrical optics, incident, refracted and reflected light beams travel in the same plane. The actual light beam has a degree of freedom for polarization (spin). When a circularly polarized light (with spin directed forward or backward), the traveling direction changes by refraction, and the angular momentum of spin also changes. However, if two media are sufficiently extensive in comparison to the diameter of light beam, the angular momentum in the direction perpendicular to the interface has to be conserved. In order that both the law of refraction and the law of angular momentum conservation hold, it is necessary to build up a new basic theory of geometrical optics in consideration of the degree of freedom for polarization (spin). The present study revealed that the degree of freedom for polarization (spin) could be taken into geometrical optics in the form of geometrical phase (Berry phase) inevitably associated with spin-involving wave. In Figs. 4 and 5, the difference in trajectories of light beam between the conventional geometric optics and the optical Hall effect is illustrated.

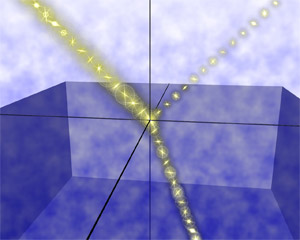
Fig. 4.

Fig. 5.

Fig. 4 shows the trajectory derived from the conventional geometrical optics, and Fig. 5 that in consideration of the degree of freedom for polarization (spin). As mentioned earlier, the conventional geometrical optics states that incident, refracted and reflected beams travel in the same plane. On the other hand, when the degree of freedom is taken into consideration, the plane of refracted and reflected light is shifted from that for incident light, as illustrated in Fig. 5. More specifically, the light beam is shifted in the direction perpendicular both to change in refractive index (normal to the boundary) and the direction of propagation. This phenomenon is to be termed as optical Hall effect. This means that Snell’s law for refraction and reflection of light is to be revised, requiring a significant change in the fundamental of physics.

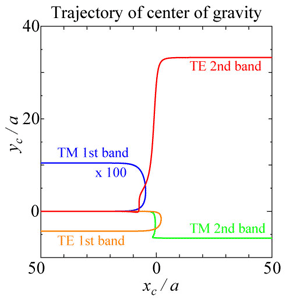
It may be suspected why such a simple effect has not been demonstrated so far with decisive experimental data. This is because the magnitude of shift is as small as the wavelength of light, generally far smaller than the diameter of light beam, which is exaggerated in the above illustrations for the sake of explanation. Another merit of the present study is to have magnified this elusive effect drastically by use of photonic crystal recently attracting broad attention. As mentioned before, the optical Hall effect is closely related to geometrical phase, Berry phase. It has been known that the Berry phase is derived not only from the inherent inner angular momentum such as spin, but also from wave undergoing periodic potential modulation such as electron in solid, only if certain conditions are met. Light traveling through photonic crystal which involves periodic modulation of refractive index, is expected to have Berry phase derived from potential modulation. In fact, a simulation using a 2-dimensional crystal without inverse symmetry, i.e., symmetry of inversion with respect to the origin, showing two-dimensional periodicity and is uniform in the direction of thickness (Fig. 6), makes Berry phase discernible. The trajectory of light beam within the photonic crystal is computed by applying the basic equations to this case, and shown in Fig. 7. Light within the 2-D photonic crystal has band structure just like electron in solid, and if the velocity in the direction of thickness is zero, the structure is divided into two modes. The mode and band index are shown by symbols in the figure. As the light beam has a finite width, the coordinate weighted with light intensity (energy) is used for the trajectory of light beam. According to the theory of relativity, mass is equivalent to energy, and the figure title is written as “trajectory of center of gravity” Photon which has zero mass but finite energy, is affected by gravity. In place of interface for the reflection and refraction problem, gradual modulation of refractive index with finite width is superimposed to the periodic modulation in this computation. Ordinate and abscissa axes are graduated with lattice constant, and if the wavelength of light were assumed to be comparable to the lattice constant, the magnitude of shift would be as large as scores of wavelength.

Fig. 6
	Fig. 7