- 確率密度関数のみを使って表される従来の式の問題点を克服する、新しい公式を考案
- 分子の形の表示法に依存せず自由エネルギー地形を計算することが可能に
- 触媒反応やタンパク質の折りたたみ反応のメカニズム解明や創薬の分野へ貢献
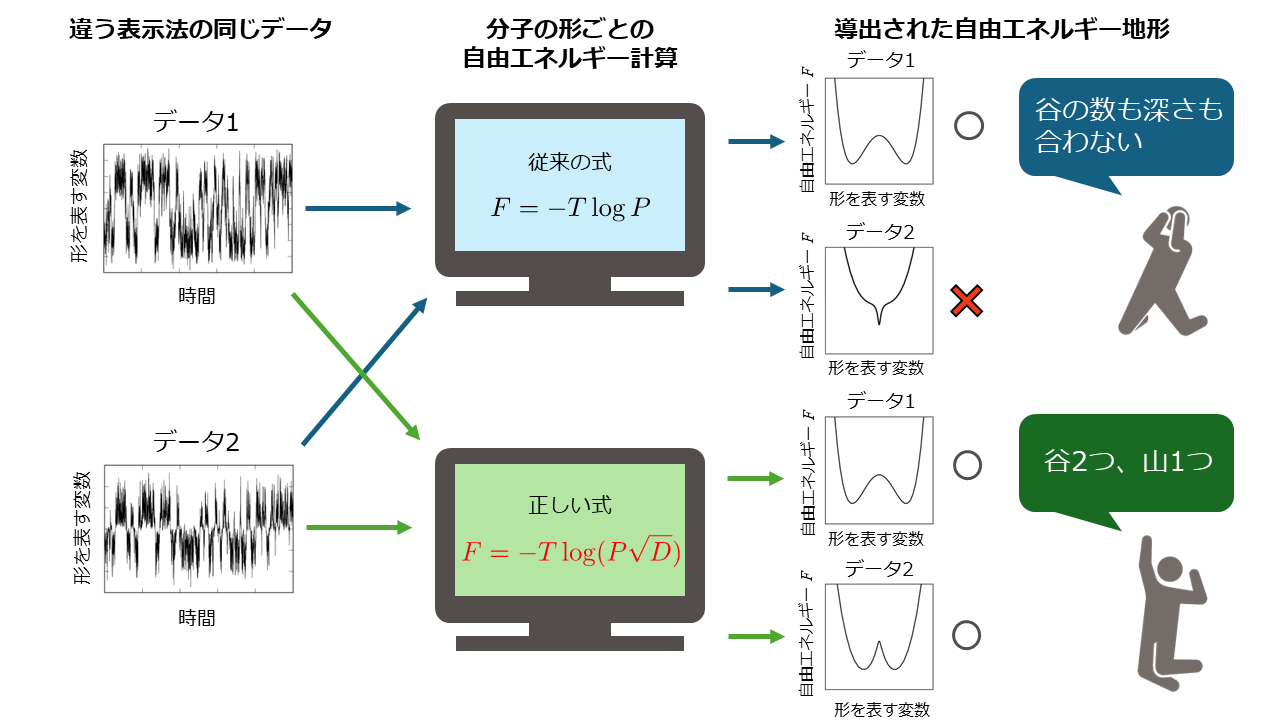
正しい自由エネルギー地形は分子の形の表示方法に依存せず谷の数や深さを評価することができる。
国立研究開発法人 産業技術総合研究所(以下「産総研」という)機能材料コンピュテーショナルデザイン研究センター 材料インフォマティクスチーム(兼 産総研・東北大数理先端材料モデリングオープンイノベーションラボラトリ)中村 壮伸 主任研究員は、反応座標の表示法に依存しない自由エネルギー地形の計算手法を確立しました。
自由エネルギー地形は、設計した触媒の反応が期待通りに進むことをシミュレートしたり、薬効や副作用を予測して医薬品の開発に生かしたりするなど、幅広い分野で活用されています。しかし、従来の手法では、化学反応における分子の立体構造変化の表示方法に依存して異なる自由エネルギー地形を導出してしまうため、定量的な予測や解釈の理論的根拠が薄弱でした。
本研究では分子の変形運動を、ブラウン運動を記述するときに用いられるランジュバン方程式で表現しました。そこに現れる拡散係数を用いることで、形を表す変数の表示方法によらない自由エネルギー地形を導出することに成功しました。この研究成果は、触媒反応やタンパク質の折りたたみ反応について定量的な議論をする上での理論的基盤を定めます。本研究成果の公式を用いることで、触媒や医薬品の設計に際して根拠となる質の高いデータを提供できるようになると期待されます。
なお、本研究成果の詳細は、2024年3月27日(米国東部夏時間)に、米国物理学会の学術誌「Physical Review Letters」の電子版に掲載されました。
自由エネルギーは、タンパク質の折りたたみや触媒反応を記述する際の基本的な物理量であり、分子の反応性を示します。安定な形状のタンパク質では自由エネルギーが低くなります。反応や折りたたみの際には分子の形が変化し、それに応じて自由エネルギーも変動します。自由エネルギー地形は、分子の取りうる形ごとの自由エネルギーを等高線のように表したものであり、反応の熱力学的性質と動力学的性質を結びつける重要な物理量です。
ところが、従来用いられていた自由エネルギー地形の定義は、物理量が満たさなければならない不変性を持たないため、問題があることが知られています。例えば同じ角度を表す場合でも、単位円の弧長θ[ラジアン]や余弦χ=cosθのようにいくつかの異なる表示方法がありますが、いずれの表示方法を用いたとしてもそこから得られる物理的性質は不変でなければなりません。当然、分子の形が変化したとき、反応の起こりやすさなどを表現する自由エネルギー地形は、分子の形の表示方法に依存せず不変であるべきです。しかし、従来用いられていた自由エネルギーの定義は、θやχのいずれを選ぶかなどのように、どのような表示方法を用いるかで異なる結果が得られていました。
数学的に、表示方法に依存せずに値がきまるという性質を持つ量をスカラーと呼びます。つまり、従来用いられている自由エネルギー地形はスカラーでない量として定義されていました。この事実は、分子が安定な形から別の安定な形に変形する際の自由エネルギー変化を客観的な物理量として計算できないことを意味しています。従来の定義を用いる限り物理化学的な議論には客観性が担保されておらず、タンパク質の折りたたみ反応や触媒反応、創薬などさまざまな分野においてシミュレーションや実験で得られたデータの解釈を見誤る可能性がありました。
本研究では、物理法則の満たすべき条件である共変性に注目しました。共変性とは、例えば物理法則を角度で表す際に、変数として単位円の弧長θで表しても余弦χ=cosθで表しても、角度から定められる物理法則そのものは変わらないことを保証するような原理です。重力やブラックホールなどを記述する一般相対性理論でも共変性が使われています。粘弾性体の構成方程式を記述する際には、共変性は物質客観性原理という別名で使われています。重力であろうと粘弾性体であろうと、触媒やタンパク質の折りたたみ反応であろうと、物理現象を記述する以上は共変性を満たす必要があります。
なお、本研究は独立行政法人 日本学術振興会の科学研究費助成事業(15K13530、19H01864、18H01188)による支援を受けています。
従来の自由エネルギー地形は出現頻度(確率密度関数)つまり、データの疎密P(θ)の対数(log)に-Tをかけたもの(Tは絶対温度)として導入されています。
-T logP (θ)
この定義に従うと、形を表す変数を θで表示するかχで表示するかによって値が変わってしまいます。実際、χにおけるデータの疎密を用いると-T logP (χ)ですが、P(θ)とP(χ)の間には
P(χ)=P(θ)dθ/dχ
という関係がありdθ/dχの分ほど一致しません。自由エネルギー地形はT log(dθ/dχ)だけ違ってしまいます。
本研究が採用したアイデアは世界地図上に人口密度のデータを重ねることを考えることに例えると理解しやすいです。人口密度が自由エネルギー地形に当たります。実際の人口密度はどんな地図を使うかによらず不変でなければなりません。しかし、データを適切でないやり方で処理してしまうとそのようにならないことが起こり得ます。これが従来の自由エネルギー地形の問題点そのものです。
例えば図1の灰色枠内の絵のように地図上に人が点として分散している状況を考えましょう。上の円弧が地球儀の南北を横に寝かせた地図、下の線分が地軸に垂直な方向から投影して作った地図とします。後者では極の近くの面積が小さく縮小されてしまうため、ある地域の点の数をその地域の地図上の面積で割ることで得られる見かけの人口密度は、極地域では赤道地域(中央付近)よりも過大評価されてしまいます。
従来の自由エネルギー地形はこの見かけの人口密度に基づいて定量的な評価がされていました。従来の自由エネルギー地形-T logP(青枠)は地図(灰色枠)の上の見かけの点の疎密Pだけに注目していたので表し方をθ(灰色枠の上の曲線)の地図にするかχ(灰色枠の下の線分)の地図にするかによって、谷の深さが異なります(青枠の上下の図を比較)。これでは実情にそぐわない議論をしてしまいかねません。そこで、「人口密度」の担い手である「人」の「歩幅」すなわち運動の激しさで地図上の面積を規格化します。本研究では「歩幅」として拡散係数Dを用います。地図上の歩幅は極近くの人たちは相対的に小さく、赤道上では大きくなります。地図上の歩幅で規格化された人口密度は表示の選択に依存しない表し方になります。すなわち、今回開発した自由エネルギー地形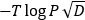 (緑枠)では地図上の場所ごとに異なる歩幅D(灰色枠の赤色矢印)で密度を規格化しているためθの地図でもχの地図でも状態Aと状態Bの谷の深さが同じになります(緑枠の上下の図を比較)。これにより地図上の見かけの人口密度が持つ問題点、すなわち従来の自由エネルギー地形の問題点は解消されます。
(緑枠)では地図上の場所ごとに異なる歩幅D(灰色枠の赤色矢印)で密度を規格化しているためθの地図でもχの地図でも状態Aと状態Bの谷の深さが同じになります(緑枠の上下の図を比較)。これにより地図上の見かけの人口密度が持つ問題点、すなわち従来の自由エネルギー地形の問題点は解消されます。
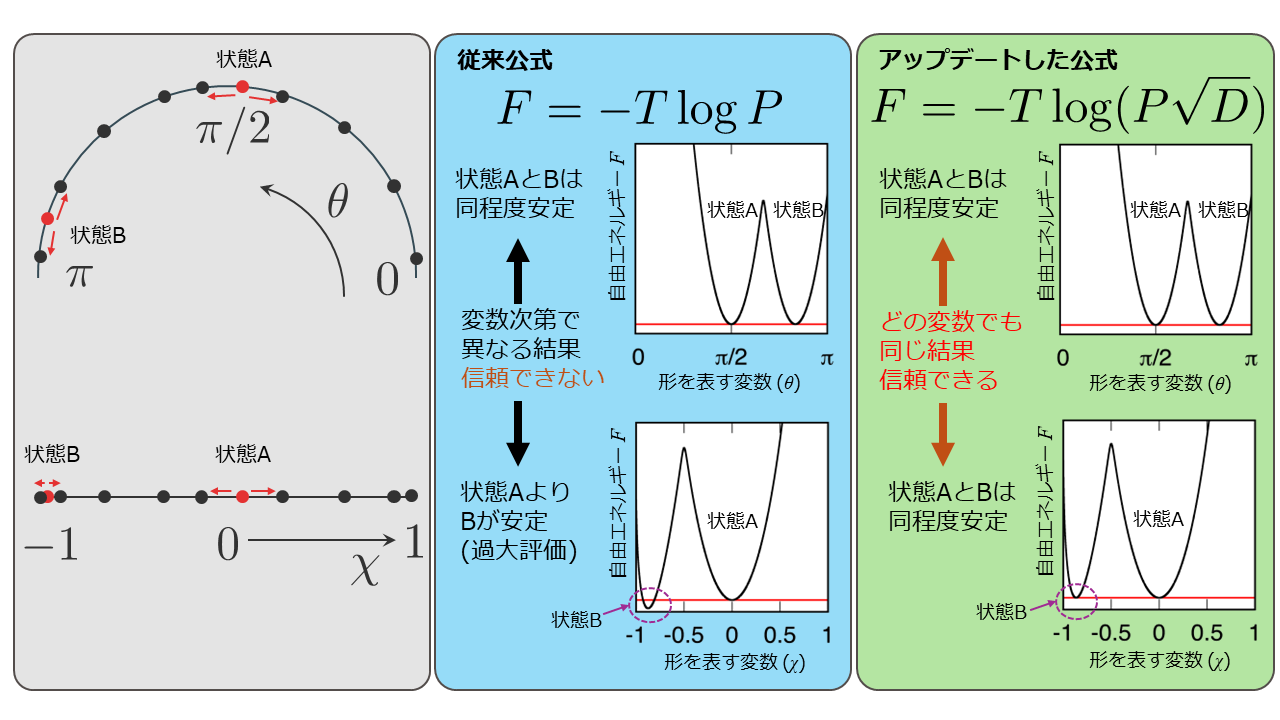
図1 地図とその上の見かけの「人口密度」(灰色枠の線とその上の点)、見かけの「人口密度」のみから計算された自由エネルギー地形(青枠)、「歩幅」(灰色枠の赤矢印)に基づいて規格化された「人口密度」から計算された自由エネルギー地形(緑枠)
本研究ではランジュバン方程式と呼ばれる確率微分方程式とリーマン多様体の性質を利用することによって自由エネルギー地形をスカラーとして理論的に導出することに成功しました。ランジュバン方程式は、ブラウン運動などの拡散運動を記述する方程式であり、拡散係数Dによって特徴づけられます。ランジュバン方程式を用いることで、曲がった空間であるリーマン多様体の各点における長さのスケールを定めることができました。これにより、形に依存した運動を共変的に記述することが可能となり、得られる自由エネルギー地形はスカラーになります。したがって、従来用いられていた出現頻度P(図2赤枠)だけでなく単位時間あたりの分子の形の変化の程度を表す拡散係数D(図2黄色枠)を用いることで、正しい自由エネルギー地形を導出できることが明らかになりました(図2緑枠)。
本研究で得られた自由エネルギー地形は、分子の構造変化や反応経路の定量化を数理的に正しさが保証された手続きに基づいて行うことを可能にします。この成果は化学反応や生体分子の機能に関する解釈を深める上で革新的な進展をもたらすことが期待されます。
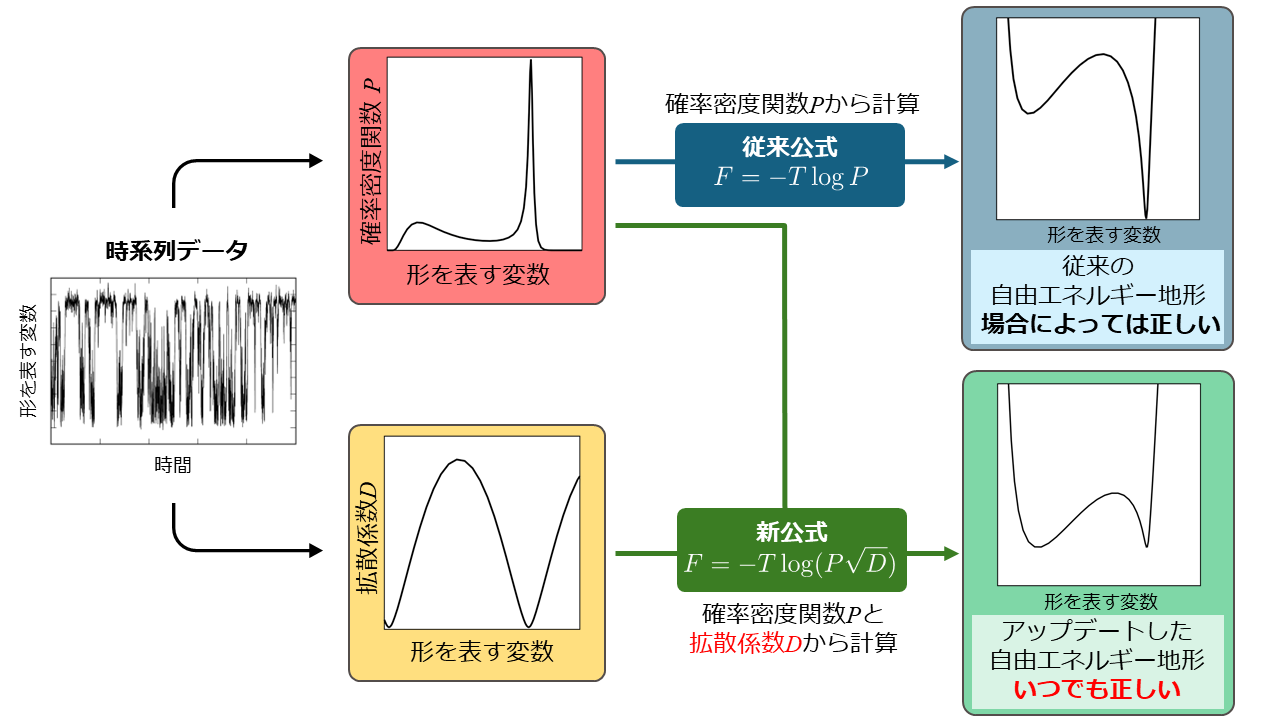
図2 与えられた時系列データから得られる量として、確率密度関数(出現頻度)P(赤枠)だけを用いているのが従来の自由エネルギー地形(青枠)です。時系列データからは拡散係数(黄色枠)も計算できます。これらを組み合わせたのが本研究で得た表示方法によらない正しい自由エネルギー地形(緑枠)です。
今後は、時系列データに基づいて状態に依存した拡散係数を計算するアルゴリズムの開発や公開などを行い、シミュレーションや実験で得られた自由エネルギー地形を用いたデータ解析の発展・応用を進めていきます。
掲載誌:Physical Review Letters
論文タイトル:Derivation of the invariant free-energy landscape based on Langevin dynamics
著者:Takenobu Nakamura
DOI:https://doi.org/10.1103/PhysRevLett.132.137101