アモルファス材料などの不規則な原子配列を表現する数理的手法を創出

　国立研究開発法人 産業技術総合研究所【理事長 中鉢 良治】（以下「産総研」という）機能材料コンピュテーショナルデザイン研究センター【研究センター長 浅井 美博】物性機能数理設計手法開発チーム 西尾 憲吾 主任研究員、同研究センター 宮崎 剛英 副研究センター長は、アモルファス材料などの不規則な原子の並び方を簡単に表記できる数理的手法を開発した。

　材料の機能を原子レベルで理解するためには、材料を構成する原子の配列を簡潔に表現する手法が必要である。特に、人間が原子の配列パターンを直感的に理解できて、意味のある情報を容易に読み取れる表現法が求められている。しかし、アモルファス材料は原子が不規則に並んでいるため、原子配列を表現することは難しい。不規則原子配列を表現する手法の一つにボロノイ多面体法がある。この方法では、原子をボロノイ多面体に置き換え、ボロノイ多面体が空間を埋め尽くすモデル（これは「ボロノイ多面体によるタイリング」と呼ばれている）として原子配列を表現する。その際の多面体の配列パターンを数列で表現できれば、対応する原子配列を表現したことになり、アモルファス材料などを計算機で取り扱いやすくなるが、これまでそのような手法はなかった。また、孤立した1個の多面体を数列で表現する方法はすでに幾つか提案されているが、異なる多面体が同じ数列をとる、数列の桁数が多いなどの問題があった。

　今回、「多面体は多角形というパーツの組み合わせで構成されて、多面体タイリングは多面体から構成されている」点に着目して、多面体や多面体タイリングを簡潔な数列で表現できる理論を創出した。

　本理論の詳細は、2016年4月11日に英国科学雑誌Scientific Reportsでオンライン公開される。

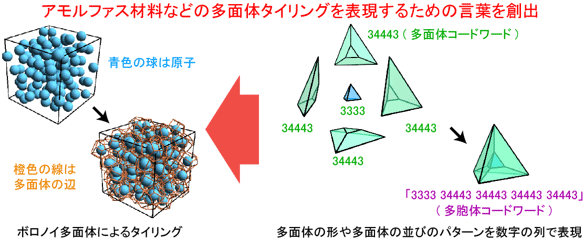
アモルファス材料の構造（左）と開発した数理的手法での表現方法（右）

　トランジスタやメモリーなどの絶縁膜や太陽電池の透明電極などには、均一な膜を容易に作製するために、アモルファス金属酸化物などのアモルファス材料が用いられることが多い。アモルファス材料の原子配列を人間が直感的に理解できる簡潔な記号で表現できれば、材料の構造と機能の関係をより深く知ることができるようになり、用途に応じて材料の化学組成などを合理的に設計することができると期待されている。

　アモルファス材料などの不規則原子配列を計算機で取り扱い、材料設計を容易にするためには、対応する多面体タイリングを簡潔に表現する数理的な手法が必要である。多面体の研究は4000年以上の長い歴史をもつが、その多くが対称性の高い多面体や多面体タイリングを対象としており、対称性のないものも含めて無限に存在する多面体や多面体タイリングを、一貫した方法で簡潔に表現する数理的手法はこれまでなかった。そのため、アモルファス構造の理解を深めるためにも不規則構造を表現するための数理的手法が求められていた。

　産総研は、計算機シミュレーションによって機能材料を設計する技術の開発に取り組んでいる。これまでにも、アモルファス金属酸化物をシミュレーションで解析し、その構造に普遍的な秩序があることを見出すなどの研究成果を創出してきた（2013年9月30日 産総研プレス発表）。

　今回、計算機を用いたアモルファス材料設計の信頼性を高めるために、その原子配列に対応する多面体タイリングを簡単に表現できる数理的手法の開発に取り組んだ。

　アモルファス材料の構造は、ボロノイ多面体が複数組み上がった構造として表現することができる。今回、「パーツを組み合わせる」というアプローチでアモルファス材料を表現しようと考えた。多面体は複数の多角形の組み合わせで作ることができるが、その多角形の組み合わせに、ある規則を発見し、その規則を利用して多面体を数列（多面体コードワードという）で表す理論を創出した。さらに、多角形というパーツを組み上げて多面体を作るという考え方を拡張すると、複数の多面体を組み上げることによって多面体タイリングを作り上げることができる。この観点から今回創出した理論を拡張すると、多面体タイリングを多面体コードワードの並び（多胞体コードワードという）で表すことができる。

　多角形、多面体、多面体タイリングは階層構造をとる。この階層構造に着目することで、多面体タイリングを表現する数理的理論を構築し、多面体タイリングを、人間が容易に理解できると同時に計算機でも取り扱いやすい形で表現することができた。

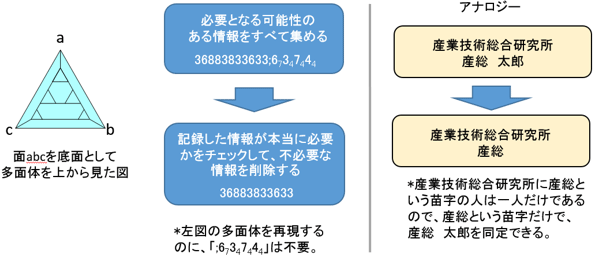
　今回の理論では、最初に、多面体を再現するために必要となる可能性のある情報をすべて多面体コードワードに記録する。その後、記録した情報の必要性をチェックして、不必要な情報を取り除く（図1）。記録した全ての情報について、必要性のチェックを繰り返すことで、これまでの手法よりも短いコードワードで多面体を表現できる。

図1 創出した理論の特徴

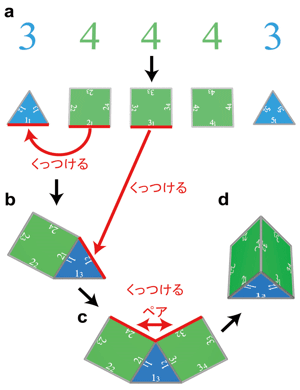
　例えば、三角柱を本理論に基づき多面体コードワードで表すと、34443となる。この数字の並びは多面体の名前であると同時に、多面体の設計図ともいえるもので、1番左端の数が3であるということは、1番目の面が三角形であることを示している。同様に、2番目から4番目の面は四角形、5番目の面は三角形であることを示す。この34443の情報から三角柱を再現する場合、次の手順で再現することができる（図2）。

　これらの手順により孤独辺が無くなり、多面体コードワード34443から三角柱を再現することができる。なお、例で示した34443以外の多面体コードワードである44343と43434からも三角柱を再現できるが、最も値の小さい34443を固有コードワードとすることで、任意の多面体に唯一の固有コードワードを割り当てることが可能となる。

図2 本理論による多面体の作り方

　概要図に示した多面体タイリングを今回の理論を用いて表すと、3333 34443 34443 34443 34443となる。多胞体コードワードの1番左端の多面体コードワードが3333であるということは、1番目の多面体が3333多面体（四面体）であることを意味している。同様に、2番目から5番目までの多面体は34443多面体（三角柱）であることを意味している。

　今回の研究は、アモルファス材料などの不規則原子配列を人間が理解できるように記述すると同時に、計算機でも取り扱いやすくすることを目的に行ったが、その結果として得られた理論は、材料開発だけではなく、学術的な観点からも有用で応用範囲も広い。例えば、この理論を応用すると、3次元の多面体だけではなく、より複雑な高次元の立体を系統的に記述できる。また、今回の理論を用いることで、複雑な構造を持つデータを計算機で効率的に取り扱えるなど、他の技術分野への波及効果も期待できる。
 

　本研究で創出した理論を用いることによって、アモルファス材料などの不規則な原子配列を短く分かりやすい数字の列で表現できるようになった。今後は、この理論を活用してアモルファス材料の構造と機能の相関を解析し、アモルファス材料を合理的に設計する手法の開発につなげていく予定である。

◆アモルファス

物質の原子配列において、結晶などで見られる周期的構造が存在せず乱れた構造をしていることを表す形容詞。非晶質ともいう。ナノメートルサイズのデバイスで結晶性の材料を使うと、多くの場合結晶構造は均一な単結晶ではなくデバイスと同じレベルのサイズの結晶粒の集合体となり、隣接する結晶粒同士の境界（結晶粒界）が発生する。ナノメートルサイズのデバイスでは結晶粒界がデバイス特性に大きなダメージを与えるおそれがある。アモルファス構造にすれば結晶粒界ができないので原子レベルで均一な構造を実現できる。[参照元へ戻る]

◆ボロノイ多面体

一つの原子Aの周りに最近接する原子との距離を二等分する面で囲まれた多面体。換言すると、A原子以外のいかなる原子との距離よりA原子との距離が短くなるような領域の全体である。また、このようにして空間の領域分割をすることをボロノイ分割という。ボロノイ多面体の形状を計測することはA原子を取り囲む原子の配列について、最近接原子数より高次の幾何学的な情報が得られるため、乱れた構造の特徴を定量的に把握するのに有用である。[参照元へ戻る]

◆タイリング

多角形で平面を充填したり、多面体で空間を充填したりすること。多面体で空間を充填した構造を多面体タイリングと呼ぶ。[参照元へ戻る]

◆コードワード

情報を表現するための記号。今回創出した理論では、多面体コードワードという数列によって多面体の形を表し、多面体コードワードを並べた多胞体コードワードによって、多面体の並びを表す。[参照元へ戻る]