独立行政法人 産業技術総合研究所【理事長 中鉢 良治】(以下「産総研」という)ナノシステム研究部門【研究部門長 山口 智彦】非平衡材料シミュレーショングループ 西尾 憲吾 主任研究員、中村 恒夫 主任研究員、宮崎 剛英 研究グループ長は、幾何学に基づく考察と第一原理計算から、アモルファス金属酸化物には金属の種類や、金属と酸素の比率によらない構造普遍性があることを見いだした。
アモルファス金属酸化物はトランジスタやメモリーなどの絶縁膜や、太陽電池の透明電極などに用いられる重要な材料である。デバイスのサイズをナノメートルサイズに縮小すると材料の構造のばらつきを原子レベルで抑えないといけないため、材料の構造を原子レベルで理解しておく必要がある。今回、金属原子と酸素原子の配列を別々に解析することにより、アモルファス金属酸化物は金属と酸素それぞれのランダム充填構造が組み合わさってできていることを予測した。
今回の成果は、電子デバイス用材料などを設計する技術の高度化に貢献するものと期待される。成果の詳細は、2013年10月3日、米国物理学会誌Physical Review Lettersにオンライン掲載される予定である。
 |
|
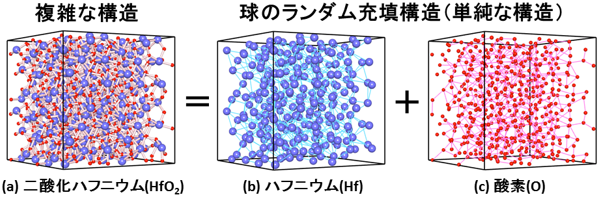
(a)第一原理計算で求めたアモルファス構造の二酸化ハフニウム(ハフニアとも呼ばれる)の原子配列。青と赤の球はそれぞれハフニウムと酸素の原子を表す。(a)の構造は(b)ハフニウムと(c)酸素それぞれのランダム充填構造が組み合わさってできている。 |
金属酸化物はトランジスタやメモリーなどの絶縁膜や太陽電池の透明電極などとして使われる重要な材料である。膜の均一性や製膜プロセスの容易性を担保するためにアモルファス構造を採用することが多い。デバイスのさらなる省電力化や高性能化を目指してデバイスサイズをナノメートルの単位まで微細化するためには、材料が原子レベルで均一であることが求められる。アモルファス金属酸化物の原子構造に対する十分な知見があれば、材料の均一性と電気的絶縁性を両立させるプロセス条件などを合理的に設計することが可能になると期待される。しかし、結晶金属酸化物と異なり原子配列に規則性を持たないアモルファス金属酸化物の原子構造は大変複雑であるため、これまでアモルファス金属酸化物の原子構造に対する包括的な理解がされていなかった。
産総研は先端材料やデバイスの開発を加速するシミュレーション技術の開発に取り組んでいる。先端材料がアモルファスの場合、原子レベルの構造情報を実験的手法だけで精度よく把握できないことがある。このため、シミュレーションを活用してアモルファス構造に対する精度の高いモデリングを行う必要がある。これまでに金属原子内包シリコンクラスターが凝集したアモルファス材料の構造モデリングを行い、クラスター構造を保ちながらアモルファスまたは液体状態のシリコンと似た構造も同時に成り立っていることを見いだした。また、直径がナノメートルサイズの細い穴の中に閉じ込められたアモルファスアルゴンの安定性の研究を行い、細い穴の中では結晶構造ではなくアモルファス構造がアルゴン固体の最安定構造であることを提案した。今回、アモルファス金属酸化物の構造を包括的に理解することを目指して幾何学的考察と第一原理計算によって系統的に構造解析した。
アモルファス構造を解明することは、元来、物性物理学における難問の一つである。図1に結晶構造とアモルファス構造の概念的な相違を示す。結晶(図1(a))では原子が周期的に配列するため、その構造を比較的容易に同定できる。しかし、アモルファス構造(図1(b))は結晶のような原子配列の周期性が無い乱れた構造であるため、ある原子を取り囲む原子の数が、決まった値をとりやすいといった最近接原子間の配置に関係する規則性(これを「短距離秩序」という)を除いて、詳細な構造情報を得ることが困難であった。アモルファス金属酸化物では金属原子の周囲の最近接酸素原子数は金属の種類や酸素含有量ごとに異なる。例えばアルミナ(Al2O3)では4と5、チタニア(Ti2)と酸化インジウム(In2O3)では共に6、ジルコニア(ZrO2)とハフニア(Hf2)では共に6と7である。このように、短距離秩序を見る限りアモルファス金属酸化物に共通な性質を見いだすことができない。そのため、これまでそれぞれの材料が包括的に調べられることはなかった。
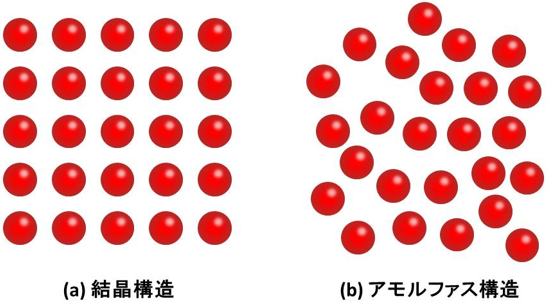 |
図1 結晶構造とアモルファス構造の違いを示す概念図
赤い球が原子を表す。 |
産総研は、金属の種類や酸素量の違いによらないアモルファス金属酸化物に共通な原子配列が存在するのか、存在するとすればどのような配列であるのかという根源的課題を追及するために、第二近接原子同士の配置における規則性(これを「中距離秩序」という)を調べた。そのため、結晶構造の幾何学的考察に立ち戻り、アモルファス金属酸化物の構造を支配する原理を議論する方法論を構築した。まず、1種類の元素からなる多くの物質においてその結晶構造は面心立方格子や体心立方格子など、球の充填率を高める構造をとる。次に結晶金属酸化物では、結晶構造を金属原子と酸素原子で別々に見ると、共に球の充填率の高い構造あるいはそれに近い構造をとっていることが分かる。例えば酸化銅(Cu2O)結晶は面心立方格子の銅原子と体心立方格子の酸素原子が組み合わさった構造を取っていると見なすことができる。この結果を一般化すると、アモルファス金属酸化物の構造も金属原子と酸素原子がそれぞれに球の充填率の高い構造をとり、両者が組み合わさってできていることが予想される。
上記の考え方を立証するため、チタン(Ti)、ジルコニウム(Zr)、ハフニウム(Hf)、銅(Cu)、アルミニウム(Al)、ガリウム(Ga)、インジウム(In)の7種類の金属を選んで、それぞれの酸化物(TiO2、ZrO2、HfO2、Cu2O、Al2O3、Ga2O3、In2O3)に対してアモルファス構造の第一原理計算を行った。
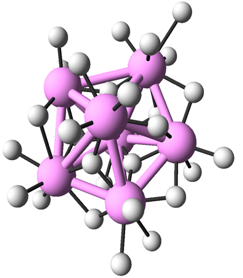
金属酸化物は結晶でもアモルファス状態でも金属と酸素原子が互いに最接近しているので、第二近接原子の構造を解析して中距離秩序を調べるには金属原子と酸素原子を別々に考えて金属同士および酸素同士の最近接原子間の構造を解析すれば良いと考えた。図2に、7つの金属酸化物のうちAl2O3で見つかった金属原子、および酸素原子の20面体配列を示す。球をランダム充填すると図3に示したような五角両錐形構造が多く含まれることが知られており、五角両錐形構造から作られている20面体構造を含むことから、アモルファス金属酸化物の構造は、金属と酸素がそれぞれ球のランダム充填構造を形成して両者が組み合わさってできていることが強く示唆される。
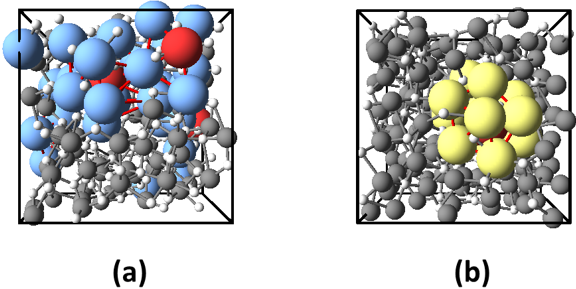 |
図2 第一原理計算で得られたアモルファスAl2O3の20面体配列
色づけされた大きな球は(a) アルミニウム原子および(b) 酸素原子の20面体配列を示す。 |
 |
|
図3 五角両錐形構造(色づけされた大きな球) |
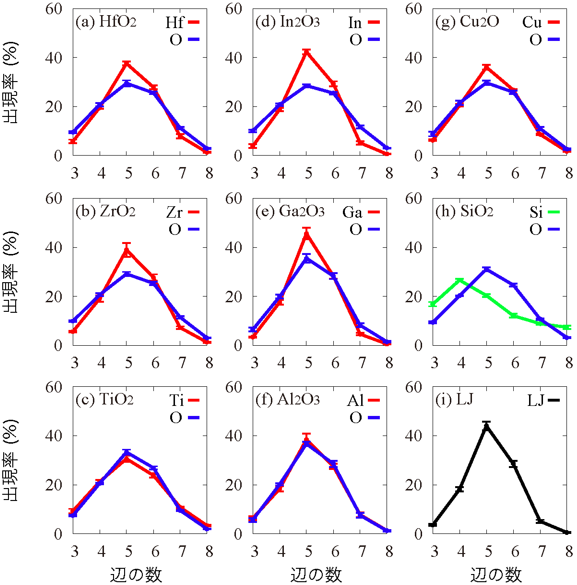
五角両錐形構造がアモルファス金属酸化物に含まれることを定量的に調べるため、最近接する金属原子間および酸素原子間の二等分面で囲まれる多面体(これをボロノイ多面体という)を計算機上で構築し、ボロノイ多面体を構成する面に含まれる辺の数を数え、面の形の分布を調べた(図4)。五角両錐形構造が多いことはボロノイ多面体が多くの5角形から作られていることに対応する。球のランダム充填構造の例としてレナードジョーンズポテンシャルで相互作用する粒子系のアモルファス構造に対しても同様の解析を行った(図4(i))。図4(a)~(g)の結果から明らかなように、金属の種類や酸素含有量に関係なく、金属と酸素ともに、ボロノイ多面体を構成する面の形は5角形が最も多く、6角形→4角形→7角形→3角形→8角形の順番に出現頻度が下がっていく。これは、図4(i)に示したレナードジョーンズポテンシャル系と同じ結果になっている。このことから、アモルファス金属酸化物の構造は、金属と酸素がそれぞれ球のランダム充填構造を形成して両者が組み合わさってできていることが分かった。
言い換えれば、今回の研究によって同物質の普遍的な構造が同定されたことになる。図4(h)に半導体Siの酸化物(SiO2)の結果を示す。シリコンネットワークのボロノイ多面体では4角形が最多であり、酸素原子のみがランダム充填構造をとる。シリコンと酸素の間の共有結合性が強いことが主な要因と考えられる。
 |
|
図4 (a)~(g) アモルファス金属酸化物における金属と酸素それぞれのボロノイ多面体の辺数分布 |
|
比較のため(h)半導体Siの酸化物(SiO2)と(i)レナードジョーンズポテンシャルで相互作用するアモルファス構造に対する解析結果も掲載する。(a)~(g)はいずれも金属の酸化物だが、(h)は性質の異なる半導体の酸化物に対する結果であるため、(a)~(g)と区別して曲線を緑色にした。 |
アモルファス金属酸化物が金属と酸素それぞれのランダム充填構造が組み合わさってできていることの定性的な理由は次のように説明される。金属酸化物では金属から酸素への電荷移動が起こり金属はプラスに、酸素はマイナスに帯電するため金属と酸素は主にイオン結合によって結合している。金属原子のネットワークから見ると、酸素原子を濃度一定のマイナス電荷と見なせる。このマイナス電荷は金属原子のプラス電荷同士の反発を和らげて金属原子のネットワークが壊れるのを防いでいる。逆に酸素原子のネットワークにとって金属原子は濃度一定のプラス電荷とみなせる。このプラス電荷は酸素原子のマイナス電荷同士の反発を和らげて酸素原子のネットワークが壊れるのを防いでいる。以上のことから、中距離秩序を支配する要因は金属のプラス電荷同士あるいは酸素のマイナス電荷同士の球対称な反発力であり、この力が球のランダム充填を引き起こすと考えられる。
今回明らかになった中距離秩序の知見を利用することで、今まで以上の高い精度でアモルファス金属酸化物の構造がモデリングでき、精度のばらつきも抑えることができるようになると期待される。今後、ナノメートルサイズの電子デバイスに使われる絶縁膜や太陽電池の透明電極など、さまざまなアモルファス金属酸化物材料の原子構造を合理的にモデリングできる手法の開発につなげていく予定である。