国立研究開発法人 産業技術総合研究所【理事長 石村 和彦】(以下「産総研」という)人工知能研究センター【研究センター長 辻井 潤一】機械学習研究チーム 麻生 英樹 研究チーム長、椿 真史 研究員と、国立大学法人 東京大学 生産技術研究所 溝口 照康 教授は、量子物理学の密度汎関数理論に基づく深層学習技術を開発した。この技術は、化合物の原子配置だけから、その電子の確率分布を表す波動関数への変換を経由して、電子密度、そしてエネルギーなどの物性値を高速・高精度に外挿予測できる。
材料開発や創薬の分野では、化合物のさまざまな物性値の計算が必要不可欠であるが、深層学習技術を用いて物性値を予測することで、計算量を抑えられることが知られている。今回開発した技術では、深層学習モデルの内部に、波動関数と電子密度という量子物理的に最も基本的な情報を顕わに表現することによって、現在深層学習で大きな問題となっている予測結果の解釈性・信頼性の問題を解決する。また、波動関数と電子密度という、データの偏りに影響されない普遍的な情報に基づくことで、学習データとは分子構造が大きく異なる未知化合物の物性を外挿予測できる。これによって、材料開発や創薬の分野における大規模な有用物質探索への貢献が期待される。
この技術の詳細は、2020年11月10日(米国東部時間)にアメリカ物理学会から出版されている
Physical Review Lettersに掲載された。
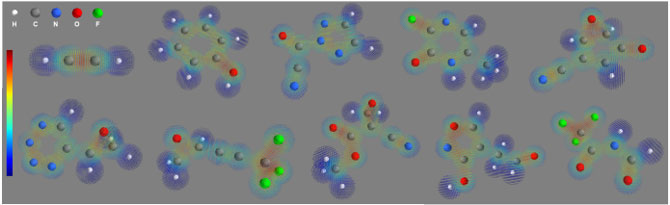
図1:開発した深層学習技術によって推定された化合物の電子密度
波動関数が得られて初めて、このような電子密度を予測し可視化できる。数秒以内で一つの化合物の電子密度が予測できる。この図では、白色が水素H、灰色が炭素C、青色が窒素N、赤色が酸素O、緑色がフッ素Fを表し、化学結合にあたる部分により電子が集まっているのがわかる(赤色で示された部分)。
材料開発や創薬の分野では、化合物のさまざまな物性値(物質のエネルギー、触媒の反応収率、発電材料の効率、薬剤の活性など)の計算・予測が必要不可欠である。その計算・予測には、量子物理学に基づく理論計算・シミュレーションが有用と認識されてきた一方で、膨大な計算コストという問題がある。これを解決するために近年、人工知能技術の一つである深層学習が用いられるようになってきた。しかしながら、理論計算・シミュレーションとは異なり、深層学習の計算の中身はブラックボックスなので、材料開発や創薬の現場で重要な解釈性・信頼性が低いことが大きな問題となっている。さらに人工知能技術は一般に、存在するデータから答えを導く内挿は得意だが、存在しないデータを推測して答えを導く外挿は不得意であり、性能が著しく悪化することが多い。例えば、物性値予測での外挿とは、学習用のデータと分子構造が大きく異なる化合物の物性予測などである。なお、内挿とはその逆で、分子構造がほぼ同じ化合物の物性予測である。外挿予測は新規の材料や薬剤の開発に極めて重要である。
産総研では、最先端の機械学習技術の理論・アルゴリズムの開発から実データへの応用まで、幅広く研究を行ってきた。その一環として、材料開発や創薬で重要な化合物の物性値予測について、高い解釈性・信頼性を持つ深層学習技術の研究開発に取り組んできた。また東京大学生産技術研究所では、機械学習技術を材料開発に利用するマテリアルズインフォマティクスに関する研究を行ってきた。その一環として、界面構造を高速に決定する手法の開発や、スペクトルから物性を予測する手法の開発に取り組んできた。
なお、本研究開発はJSPS 科研費 20K19876、MEXT 科研費 19H05787、19H00818 による助成を受けて行った。
今回開発した技術では、まず化合物Mの原子配置の情報を、理論計算・シミュレーションで用いられる原子の波動関数φに変換して、量子物理的に正しい計算の出発点を得る。次に、波動関数の重ね合わせの原理に従い、このφから分子の波動関数ψを計算する。そして、このψから物性値Eを学習する。加えて、分子の波動関数ψから得られる電子密度ρと原子配置から計算できるポテンシャルV とが一対一対応するというホーヘンベルグ・コーンの定理を、モデル全体への物理制約として課す。これらはすべて、密度汎関数理論の枠組みに基づいていることが重要な点である。このモデルを、化合物の原子配置(入力)と物性値(出力)に関する大規模データベースを用いて学習させることで、波動関数と電子密度を経由した物性値の予測が可能になる。量子物理的に最も基本的な情報であるψやρを経由して物性値が導かれるため学習データの偏りに影響されない化合物の本質を捉えることができ、物性値の外挿予測が可能になる。具体的には、分子の波動関数ψから物性値Eの予測を行うニューラルネットワークと、電子密度ρにポテンシャルVの制約を課すニューラルネットワークという、二つのニューラルネットワークを交互に学習する。ψとEを繋ぐ関数と、ρとVを繋ぐ関数は、どちらも正確な形がわかっていない複雑な関数であり、これらを大規模データベースから学習する。図2に、この深層学習モデルの概略図を示す。
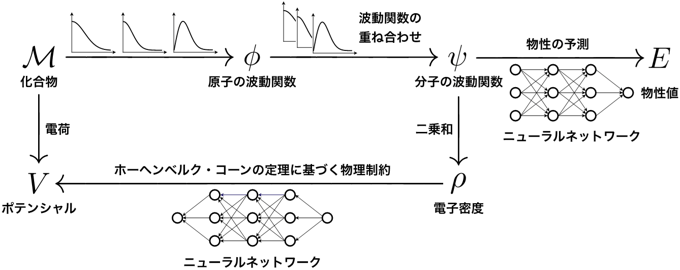
図2:今回開発した深層学習モデルの概略図
今回の技術で得られた分子の波動関数から電子密度を計算し、可視化したのが図1である。これらの電子密度は、理論計算・シミュレーションの結果と比較して妥当であった(図3)。理論計算で得られる値は実験で得られる値を1〜2kcal/molの誤差で予測できる一方で、今回の技術はその理論計算値を1〜3kcal/molの誤差で予測できる。つまり、実験値を2〜5kcal/molの誤差で外挿予測できることになり、これは従来技術よりも高い精度であり充分実用に耐えうる精度と言える(図4)。さらに、理論計算は1種類の分子に数十分から数時間かかるが、今回の技術は数分で1万種類の分子を予測できる。このように、実用に耐えうる外挿精度を保ちながら理論計算を10万倍以上高速化した今回の技術は、新規の材料や薬を大規模に探索し効率的に発見・開発するという実応用では重要となると考えられる。
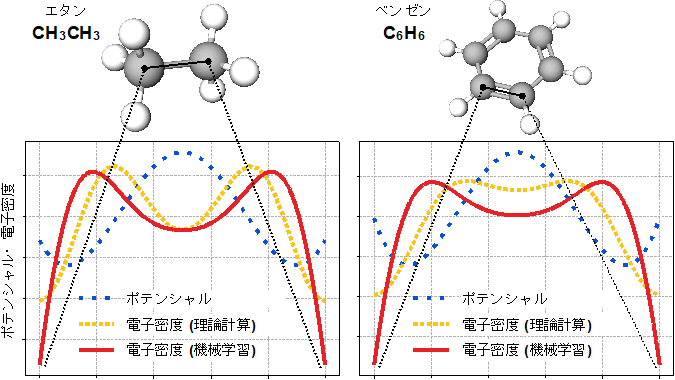
図3:今回の機械学習と理論計算で得られたエタンとベンゼンの化学結合の電子密度の比較
理論計算で得られる電子密度には二つのピークがあり、今回開発した機械学習でもその二つのピークを再現できた。
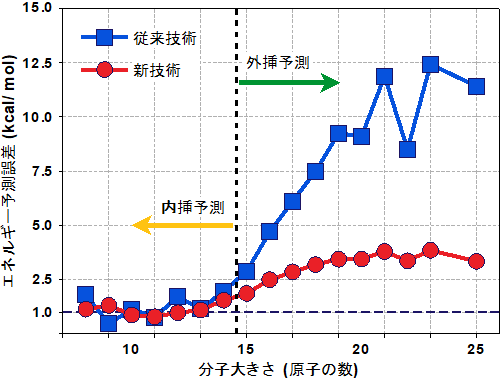
図4:物性値(エネルギー)の外挿予測精度
横軸は分子の大きさを表し、学習用のデータには14原子以下の分子だけを用いている。縦軸はエネルギーについての理論計算と予測結果との誤差を示し、小さいほど理論に近い精度で予測できていることになる。今回開発した機械学習技術では、分子が20原子以上と大きく未知で複雑な構造になっても、予測誤差を小さく保てている。
今回開発した技術の大きな特徴は、密度汎関数理論に基づき、波動関数と電子密度を深層学習モデルの内部で表現・経由した上で、化合物の物性値を予測する点である。このように、物理理論の理解に基づくことで深層学習モデルのブラックボックス性が解消され、材料開発や創薬の実応用の際の解釈性・信頼性が向上する。
今後は、材料開発や創薬の実応用で今回開発した技術を用い、有用な触媒や薬剤の大規模な探索を行う。また、物理学者・化学者と協力して、物理学・化学に関する知識をより多く取り入れ、より高精度の予測ができる深層学習技術の開発を目指す。
雑誌名:Physical Review Letters
論文タイトル:Quantum deep field: Data-driven wave function, electron density generation, and energy prediction and extrapolation with machine learning
著者:Masashi Tsubaki and Teruyasu Mizoguchi