アルミ系近似結晶で半導体を創製

準結晶（注1）に半導体が存在するかどうかは固体物理学の基本的な問題の一つであり、もし存在すれば高性能熱電材料（注2）としての活用が期待されます。しかし従来、多くの準結晶が存在するアルミ系では、前駆物質である近似結晶（注3）でも、半導体は見つかっていませんでした。今回、東京大学大学院新領域創成科学研究科、および、産総研・東大 先端オペランド計測技術オープンイノベーションラボラトリの木村教授らは、アルミ系近似結晶で、バンドエンジニアリング（注4）により半導体を創製することに成功しました。これは、半導体準結晶実現への突破口となる成果で、半導体準結晶は熱電性能が結晶の2.5倍になる可能性があります。

準結晶は100種類以上の物質で見つかり、結晶、アモルファスと並ぶ固体構造の概念として確立し（表1）、2011年にノーベル化学賞に輝きました。一方、固体物理学における最も基本的な分類では、電気的性質により、金属、半金属、半導体、絶縁体に分類されます。しかし、原子スケールの準結晶には金属しか見つかっておらず（表2）、半導体や絶縁体が存在するかどうかは、固体物理学の基本的な問題の一つになっています。

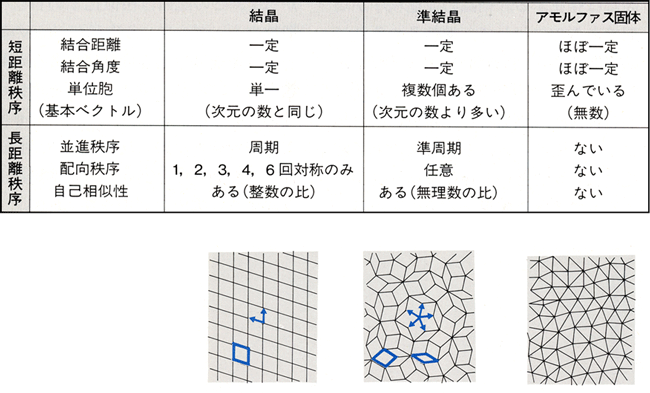
表1．結晶、準結晶、アモルファスの比較。

表2．固体の構造と電気的性質による分類。（　）内は、準周期のスケールが原子スケールより一 桁から二桁大きいものです。「？」は、原子スケールの半導体や絶縁体の存在の有無が未解明であることを示しています。

石油などの一次エネルギーの約7割は廃熱として捨てられています。この廃熱から電気エネルギーを取り出すことのできる熱電発電は非常に魅力的です。熱電性能（注5）の高い物質として、近年、結晶で最も対称性の高い立方晶で、伝導帯下端や価電子帯上端が波数空間上の多くの点にある、マルチポケット半導体（注6）が注目されています。正20面体準結晶は、立方晶より2.5倍高い対称性を持っており、半導体が実現できれば、熱電性能の出力因子も2.5倍高くなる可能性があります。

今回、アルミ系正20面体準結晶の前駆物質であるアルミ系近似結晶の一つであるAl₂₂Ir₈（図1）が、過去の第一原理計算（注7）の結果、半金属的バンド構造を持つことに注目しました。まず、その伝導帯の下端と価電子帯の上端の電子軌道の起源を調べました。その結果、図2のように、伝導帯の下端は正20面体クラスターの頂点に位置するIrのd軌道からできており、価電子帯の上端は正20面体クラスター内部のAlが8個とIrが１個からなるクラスターのp様軌道からできていることが分かりました。そこで、バンドギャップを開くために、d軌道のエネルギーがIrより高いRuでIrを置換し、sp軌道のエネルギーがAlより低いSiでAlの一部を置換したAl₁₈Si₅Ru₈の構造で第一原理計算を実行しました。その結果、予想通りにバンドギャップが広がり、半導体的なバンド構造になりました。

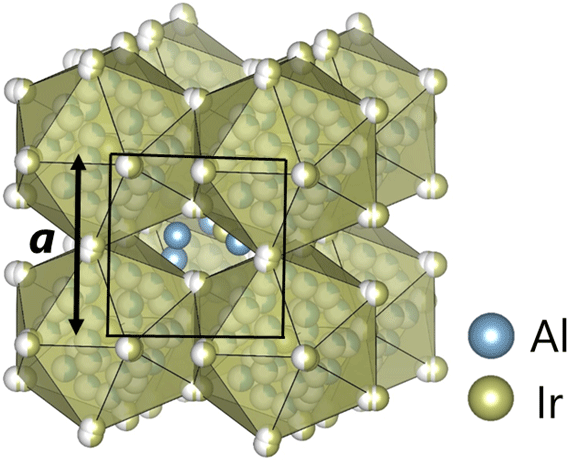
図1．Al22Ir8近似結晶の結晶構造。Irの正20面体クラスターが立方晶を作っています。

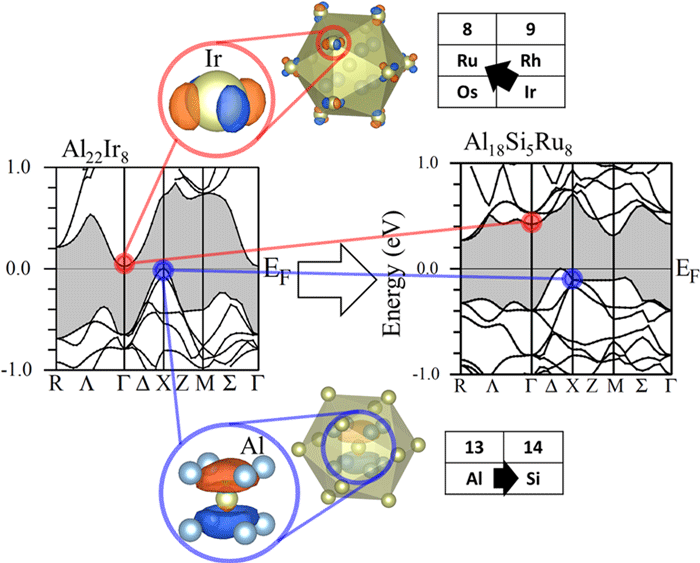図2．Al22Ir8とAl18Si5Ru8近似結晶のバンド構造と伝導帯下端と価電子帯上端の電子軌道。 IrのRu置換とAlのSi置換によるバンドエンジニアリングにより、バンドギャップを開くことに成功しました。

半導体になることを実験的に確かめるために、Al₁₈Si₅Ru₈（Al_58.1Si_16.1Ru_25.8）の組成近傍で試料を合成したところ、Al_67.6Si_8.9Ru_23.5の組成で、単相の近似結晶の作製に成功しました。この試料の熱電性能（ゼーベック係数、電気伝導率、熱伝導率）を測定したところ、ゼーベック係数、電気伝導率の温度依存性から、この試料が約0.15eVのバンドギャップを持つ半導体であることが分かりました。したがって、第一原理計算では多くの半導体が予測されていたにも拘らず実験的には実現していなかったアルミ系近似結晶で、世界で初めて、実験的に半導体を創製することに成功しました。

多くのアルミ系合金で、近似結晶の近傍組成で準結晶が生成することから、Al-Si-Ru系で半導体準結晶が見つかる可能性もあり、実現すれば最初に述べた固体物理学の基本的な問題の一つが解決でき、さらに高性能な熱電材料の開発に繋がることが期待されます。（現時点では、まだ近似結晶であり、キャリア密度の最適化もされていないので、高い熱電性能は実現されていません。）

岩崎 祐昂（東京大学 大学院新領域創成科学研究科 物質系専攻 博士課程１年生）
北原 功一（東京大学 大学院新領域創成科学研究科 物質系専攻 助教／産総研・東大 先端オペランド計測技術オープンイノベーションラボラトリ 協力研究員）
木村 　薫（東京大学 大学院新領域創成科学研究科 物質系専攻 教授／産総研・東大 先端オペランド計測技術オープンイノベーションラボラトリ 客員研究員）

雑誌名：「Physical Review Materials (Rapid Communication)」（オンライン版：6月7日）
論文タイトル：Experimental realization of a semiconducting quasicrystalline approximant in Al–Si–Ru system by band engineering
著者：Yutaka Iwasaki*, Koichi Kitahara and Kaoru Kimura
DOI番号：10.1103/PhysRevMaterials.3.061601
（アブストラクトURL：）オープンアクセスURL：https://journals.aps.org/prmaterials/pdf/10.1103/PhysRevMaterials.3.061601 [PDF: 720KB]

（注1）準結晶

結晶、アモルファスと並ぶ固体構造の一分類です。二百数十年前から三十五年前までは、原子が規則的つまり周期的に配列した結晶と不規則に並んだアモルファスの二分類しかありませんでした。ところが、原子が規則的ではあるが周期を持たずに並んだ構造が発見され、準結晶と名付けられました。結晶では許されない5回対称性や、正20面体対称性などの回転対称性を持ち得ます。表1に結晶、準結晶、アモルファスの比較を示します。その後、主に金属間化合物で多く見つかってきましたが、最近は高分子や酸化物でも見つかり、固体構造の普遍的な概念になりました。三十五年前の最初の発見者である、イスラエルのShechtman先生が、2011年のノーベル化学賞を受賞されました。ところが、表2に示すように、原子スケールの準結晶には金属しか存在せず、固体物理学における基本的な分類である電気的性質において、半導体や絶縁体の準結晶は見つかっていません。これらが存在するかどうかは固体物理学の基本的な問題の一つになっています。[参照元へ戻る]

（注2）熱電材料

材料の両端に温度差があると電圧が生じて電力として取り出すことができ、逆に、電圧をかけて電流を流すと温度差が生じる材料です。後者の性質を利用して、電子デバイスの冷却やワインセラー等、精密な温度制御に実用化されています。前者の性質で実用化されているのは熱電対温度計ですが、最近、廃熱発電の実用化に向けて、性能の高い材料の探索が世界的に盛んに研究されています。[参照元へ戻る]

（注3）近似結晶

準結晶の構造は、正20面体クラスターなどの構造単位が、準周期的に並んだものです。同じクラスターが周期的に並んだ結晶が、近似結晶です。周期が長くて、より準結晶に近いものほど、近似度の高い近似結晶と呼ばれます。準結晶と近似結晶は、構造単位が同じなので、近い組成で生成することが多くなります。[参照元へ戻る]

（注4）バンドエンジニアリング

第一原理計算（注7）により固体中の電子の状態であるバンド構造を計算し、その結果を利用して、バンドギャップの大きさやバンドの形を制御して、その固体の使用目的に対する性能を向上させる方法です。[参照元へ戻る]

（注5）熱電性能

ゼーベック係数（熱起電力）の2乗と電気伝導率をかけたものを出力因子と呼び、これに絶対温度をかけて熱伝導率で割ったものを無次元性能指数と呼びます。熱電発電の効率は、無次元性能指数が大きいほど大きくなります。熱起電力が大きいほど良いですが、電力として取り出すためには電気伝導率も大きい必要があります。また、材料中を熱が流れてしまうと温度差が無くなってしまいますので、熱伝導率は低い方が良いです。[参照元へ戻る]

（注6）マルチポケット半導体

通常、キャリア密度が大きくなると電気伝導率は高くなりますがゼーベック係数は小さくなり、キャリア密度が小さくなるとゼーベック係数は大きくなりますが電気伝導率は低くなり、最適なキャリア密度で熱電性能の出力因子は最大になります。これは、半導体のバンドにキャリアポケットが一つの場合で、キャリアポケットが複数になると、ゼーベック係数を小さくすることなく、キャリアポケットの数だけキャリア数が大きくなって電気伝導率を大きくできます。キャリアポケットの数は、対称性が高いほど多くできる可能性があり、結晶では最も対称性が高いのは立方晶です。これに対して、準結晶で可能な正20面体対称では、対称性が立方晶の2.5倍高く、ポケットの数、すなわち出力因子も2.5倍高くできる可能性があります。[参照元へ戻る]

（注7）第一原理計算

固体や分子の電子状態を求めるのに、実験値と合わせるためのパラーメーターを使わずに、量子力学の方程式を解いて計算する方法です。[参照元へ戻る]