離散化数値解法によらない並列処理用共通ソフトウェアプラットフォームを無償提供開始

　独立行政法人 産業技術総合研究所【 理事長 吉川 弘之 】（以下「産総研」という）計算科学研究部門【 部門長 寺倉 清之 】連続体モデリング研究グループ【 グループ長 手塚　明 】と、株式会社富士総合研究所【 取締役社長 伊藤 新造 】（以下「富士総研」という）計算科学技術研究センター【 センター長 松原　聖 】は、有限要素法、差分法、有限体積法等、既存の非並列離散化数値解析プログラムを、並列解析を専門としない一般的な研究者・実務者（以下「ユーザー」という）自身が、容易に並列化可能な並列処理用共通ソフトウェアプラットフォームを開発し、ユーザーへのソースコード・マニュアルの無償提供を開始^＊する。

　本ソフトウェアプラットフォームは、離散化数値解析手法の種類に依存せず、並列計算に関する高度な知識や経験なしに、高い並列化効率で並列化可能であることが特徴である。

　今後、ユーザーの協力を得て、より多くのデモプログラムを具備させる予定であり、また、より多くのユーザーが本プラットフォームによる恩恵を受けられるように、固有値解析への拡張等、その守備範囲を拡大していく予定である。

　本ソフトウェアは、新エネルギー・産業技術総合開発機構（NEDO）の研究開発事業「 研究情報基盤研究開発：離散化数値解法のための並列処理ソフトウェア技術開発【平成１１年度～】 」と、産総研先端情報計算センター（ＴＡＣＣ）の研究課題「 離散化数値解法のための並列プラットフォーム開発 」により、産総研と富士総研によって共同開発されたものである。

＊「研究情報基盤研究開発課題および高性能計算機利用促進課題の成果発表会」にて発表後、公開予定。
　　日時：平成14年3月4日(月)9:30～　場所：産総研つくば中央第2 ＯＳＬ 第6会議室（ 2階 ）＆ 1階ロビー

　製造業の活性化には、市場のニーズを反映した高付加価値製品の多品種少量生産に対応した設計プロセスの短縮が急務である。電子計算機の高性能化・低価格化を背景に、従来の試作品製作と実験による試行錯誤的・経験的な検証が数値シミュレーションに代替され、開発費用の低減と開発期間の短縮が達成されつつあるが、未だ数値解析の精度・解析スピードは、そのニーズに比較して十分とは言えない。

　計算力学の研究者・実務者は、このニーズに応えるために数値シミュレーションのソフトウェアを開発しているが、これらのソフトウェアでは往々にして研究者・実務者ごとに異なる数値解法や独自の計算手法（アルゴリズム）が使われている。これらのソフトウェアの実行には、１ＣＰＵ構成の計算機では力不足なことがあり、複数のＣＰＵでの並列高速大規模解析が必要な局面が多々あるが、多くのソフトウェアは非並列計算用に書かれているので、並列化にはプログラムの書き換えが必要である。並列化のための書き換え作業は、並列計算の経験のない研究者にとって難しく、かといって並列化作業を専門とするソフトウェア技術者に依頼しても、個別の解析アルゴリズムが理解できないために並列化作業が滞る場合が多い。その結果、計算力学の研究者・実務者にとって並列計算の敷居は非常に高いというのが現状である。

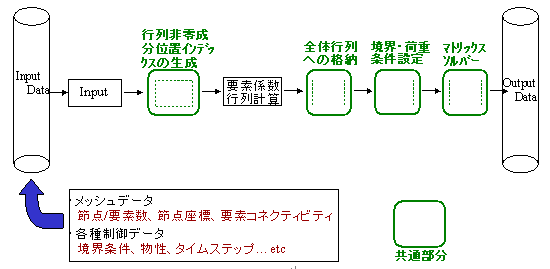
　数値シミュレーションで使用される数値解法の多くは、有限要素法、差分法、有限体積法など解析対象を格子や要素といった小さな領域に分割し、それぞれの領域における力や熱の釣合平衡方程式を、全ての領域で連立させて解くことにより複雑な形状の解析対象における物理現象のシミュレーションを行う、いわゆる離散化数値解法である。離散化数値解法では、格子や要素の数を増やすことにより解析精度の向上が可能であるが、それに伴い解くべき方程式数も大きくなり、１ＣＰＵの計算機の記憶容量及び計算能力の限界を越えるため、前述の通り高精度なシミュレーションの実行にはより大きな記憶容量と計算能力を有する並列計算機での実行が必要とされる。これらのソフトウェアの計算時間の大半は連立方程式を作成し解くといった作業のために費やされるため、この部分を並列化することにより大幅なパフォーマンスの改善が期待できる。連立方程式行列を構成するアルゴリズムは個々の解析手法によって異なるが、連立方程式行列の作成プロセスと行列を解く計算のアルゴリズムは、全ての離散化解法に共通【図１】であるため、この部分の並列化のソフトウェアテンプレートがあれば構造解析・流体解析を問わず、研究者・実務者が開発したソフトウェアについて共通に並列化を行うことができる。

　このように計算力学の研究者・実務者自身により、容易に並列化が可能となる並列処理ソフトウェアプラットフォームのニーズは非常に大きい。

図１　非並列計算用離散化数値解析のデータ・演算の流れ

　本プラットフォームの利用により、数値シミュレーションの研究者・実務者は、数日の内に大規模高速並列数値計算を実行することが可能となり、産業界に有効な、より現実に即した大規模実用解析の研究が促進される。短期的収益重視の昨今、多くの企業では、コスト削減の目的で自社開発の数値解析ソフトウェアの代わりに欧米開発の商用ソフトウェアに代替させる例が多々見られるが、商用ソフトウェアのブラックボックス的使用は企業内解析技術の退化につながり、過度の外国製ソフトウェアへの依存は、我が国の産業技術力基盤の喪失を意味する。本プラットフォームを企業実務者が導入する事により、企業内で独自に開発されて来たインハウスのソフトウェアの高速化・大規模化による性能のアップグレードが即日可能である。

　近年のPCの低価格化により、スーパーコンピュータと同等の性能を持つPCクラスタが、数百万円で購入可能である。本プラットフォームの導入により、中小企業においても大企業と同等の解析技術を手にする事ができ、日本のものづくり産業の競争力の強化が可能と考える。

特徴１　手法を選ばない並列化ソフトウェア
　離散化数値解析手法に共通な係数行列作成と行列解法に着目した並列化ソフトウェアプラットフォームなので、手法の違いによらず並列化が可能である。

特徴２　自由なレベルの並列化が可能
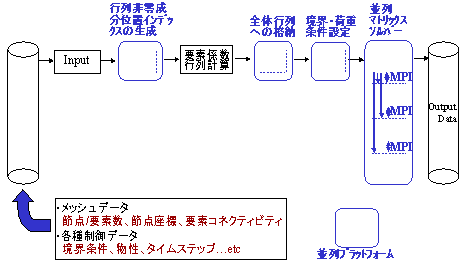
　マトリクスソルバーのみの並列化レベル１【図２】と、より大規模で高速解析が可能な数値解析全体の並列化レベル２【図３】を用意し、ユーザーのレベル、ニーズに合わせた並列化が可能である。

特徴３　要素単位による理解しやすい並列データ構造
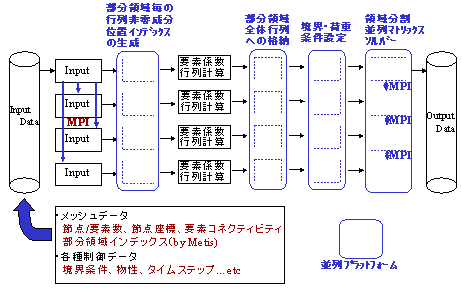
　数値解析全体の並列化の場合には要素（計算セル）に対する領域分割法の考え方で並列化し、有限要素法、有限体積法、有限差分法のいずれの数値解法にも適用できる並列化ソフトウェアプラットフォームである。

特徴４　書き換え方法が簡単
　付属のデモプログラム・マニュアルを参考に、自作プログラムに、コピー&ペーストで数行のサブルーチンプログラム（subroutine call文）を書き込むだけで並列化が可能である。

特徴５　マトリクスソルバーの選択が可能
　マトリックスソルバーは非対称行列に対応し、反復法として流体解析問題に有効なGMRES法、構造解析問題に有効なBi-CGSTAB法、直接法として極度の非線形問題に有効なバンドマトリクス法が選択可能である。

特徴６　標準的なツールの使用
　並列計算ライブラリには、標準的なライブラリであるMPIを用いた。また、数値解析全体の並列化に用いる領域分割では、領域分割フリーソフトツールMETISに対応している。

図２　並列プラットフォーム：マトリクスソルバーのみの並列化レベル１でのデータ・演算の流れ（４ＣＰＵの場合）

図３　並列プラットフォーム：数値解析全体の並列化レベル２でのデータ・演算の流れ（４ＣＰＵの場合）

　ユーザーが用意すべきデータ及びサブルーチンプログラムは、有限要素解析の場合以下のとおりである。

[1] 離散化モデル
　節点情報（節点数、自由度、節点座標）
　要素情報（要素数、要素節点）
　境界条件（固定、スライド、節点拘束）
　荷重条件
　部分領域インデックス（METISによって作成可能）
[2] 要素ごとの係数マトリックス作成ルーチン

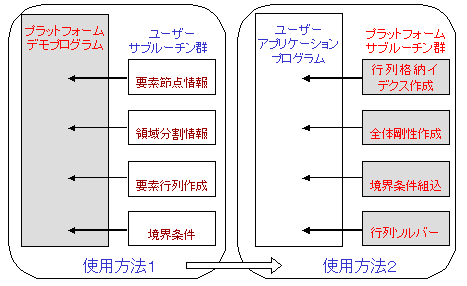
　プラットフォームにはレベル１，２それぞれに対してデモプログラムが付属しており、マニュアルに詳細な解説がされている。ユーザーはデモプログラムの一部を並列化したい解析プログラムのサブルーチンと適宜、置き換える事により、プログラムの並列化が可能である（使用方法１）。プラットフォームのより高度な利用方法として、プラットフォームのサブルーチン群をユーザーのプログラムに入れ込む事により、より柔軟な並列化が可能である（使用方法２）。【図４】　

図４　プラットフォームの使用法

　使用方法１では、レベル２の場合、以下の手順で並列化を行う。下線部が、本プラットフォームで供給される部分である。【図５】

(1)インデクス作成 　メッシュデータの情報からマトリクスの非零成分のインデクス情報を自動的に作成する。 (2)要素ごとのマトリクス係数の生成 　ユーザー作成のサブルーチンにて各要素ごとの係数マトリクスを計算する。 (3)全体マトリクスの生成 　(2)で計算した要素マトリクスから並列計算のための全体マトリクスを(1)で生成したインデクスに基づき自動的に作成する。境界条件、拘束条件の全体マトリクスへの付加を自動的に行う。 (4)マトリクスソルバー 　(3)で作成されたマトリクスを部分領域ごとに解く。

図５ 並列化手順

　既存の三次元弾性有限要素解析プログラムを、本プラットフォームを用いて並列解析プログラムに書き直し、産総研先端情報計算センター（TACC）のスーパーコンピュータ日立SR8000にて４ＣＰＵを用いて並列解析した例を示す。本プラットフォームを用いる事により、有限要素解析プログラムの並列化は数日の作業で終了した。【図６】はエンジンブロックの並列解析用モデルを示し、予め準備された六面体メッシュデータ（103061節点、89152要素）がMETISによって４ＣＰＵ用に領域分割されており、色分けされた各領域のメッシュが各ＣＰＵに割り当てられている。【図７】は並列解析によって得られた変形および等価応力図であり、Bi-CGSTABを用いて収束判定が10^-15のとき、解析に要したＣＰＵ time は1550秒である。別途、SR8000にて３２ＣＰＵを用いた検証により、並列化効率７０％以上の性能である事が確認された。

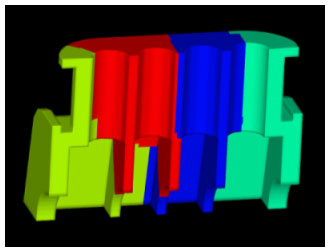
図６ エンジンブロックの並列解析用モデル

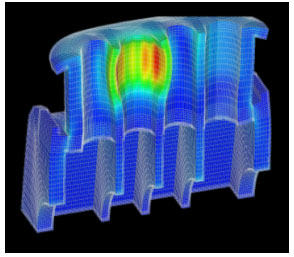
図７ 変形および等価応力図

　離散化並列数値解析のプロジェクトは、国内外に複数存在し、いくつかのものについては並列ソフトウェアのソースコードも公開されている。しかしながら、これらは自己完結したシステムの構築を主たる目的としており、ソースが公開されているもののプログラム構造が非常に複雑なため、内部のアルゴリズムを理解し、自分のプログラムとリンクさせることが困難であり、本プラットフォームのようにユーザーが開発した離散化数値プログラムの並列化を支援する用途には不向きと言える。

　前述の通り、本プラットフォームは、マトリクスソルバーのみの並列化レベル１と、より大規模で高速解析が可能な数値解析全体の並列化レベル２の二つを用意している。並列化レベル１は、並列計算機の並列数値ライブラリの行列演算ルーチンに相当するが、並列数値ライブラリはバイナリーでの供給でありハードウェア依存であるのに対し、本プラットフォームではソースコード公開であり、有効なハードウェアも１ＣＰＵ非並列計算機から分散メモリーの並列ＰＣクラスタまで対応範囲が広い。更に、部分領域間の物理量の釣り合いを基においた手法であるドメイン・デコンポジション法に基づく並列化レベル２では、並列マトリックスソルバーと比較して処理性能が高い係数行列作成部分も並列化可能なため、より大規模なモデルを扱え、より高速である。

　ユーザー自身により、計算力学ソフトウェアの並列化が数日のオーダーで可能となり、シミュレーションの処理速度が20倍以上（32ノードにて70%以上の並列化効率）になった例は他にはない。

◆有限要素法、差分法、有限体積法等、既存の非並列離散化数値解析プログラム

離散化数値解析法の種類。これらの手法は、元々、連続体である対象物を、小領域の集まりに離散化し、各々の小領域に関する方程式を連立して解くことにより、数値解を得る近似手法であり、それぞれ以下のような特徴がある。
　　有限要素法：物理量の分布を要素内で多項式関数近似する。
　　差分法：物理量の微分を差分式で近似する。
　　有限体積法：小領域（セル）の境界の物理量の出入の釣り合いを近似する。
最終的に解くべき対象は節点（要素を構成する点）、格子点（格子を構成する点）と同数の連立方程式（係数行列）となる。いずれの方法においても節点、格子点は隣り合った点と密接に関係するため、係数行列はその成分のほとんどが零の疎行列となる。近似に用いるセルのサイズは小さければ小さいほど近似の精度が良くなるため、高精度の解析を行うためには点数を増加させる必要があり、同時に解くべき方程式も大規模化する。
並列プラットフォームでは疎行列の非零成分のみを扱う事が可能である。境界要素法等、係数行列が密となる解法は本プラットフォームに適用可能ではあるが、直接のターゲットとはしない。[参照元へ戻る]

◆離散化数値解析手法（離散化数値解法）

構造物の応力-歪の関係、流れ場の速度、圧力、温度場といった空間的に広がる量を計算機によって数値的に計算する手法。上記のような値は構成方程式とよばれる偏微分方程式に従って分布するが、解析対象の形状が複雑な現実問題では、これを偏微分方程式から解析的に解くことはできないので、対象とする空間を要素や格子と呼ばれる多角形、多面体の小領域に分割し、その小領域での方程式を分布の関数近似や微分の差分近似といった近似を用いて解き、空間内に分布する節点、格子点における値を求めることによって解析領域全体の値を求める方法。離散化数値解法には有限要素法、差分法、有限体積法などがあり、有限要素法は構造解析で、差分法、有限体積法は熱・流体解析でよく用いられる。[参照元へ戻る]

◆固有値解析

行列はそれぞれ固有値と呼ばれる値を有する。振動解析では、この固有値が構造物の振動のモードと密接な関係を持つため、大規模系の固有値解析が行えることは大切である。[参照元へ戻る]

◆アルゴリズム

算法。問題を解決するための論理、または手順。プログラムの基本となる計算手法。プログラムはこのアルゴリズムに従って作成され、計算機で実行されることによって問題解決が行われる。[参照元へ戻る]

◆１ＣＰＵ

計算ユニットが１個しかない状態。１ＣＰＵの計算機では演算スピード、メモリ管理能力の限界により扱える数値解析の規模が制限される。[参照元へ戻る]

◆格子や要素

離散化解法では、連続体である解析の対象物を小さな領域からなる離散化モデルに置き換え近似するが、その小領域の名称。有限要素法では「要素」、差分法では「格子」、有限体積法では「セル」と呼ぶ。[参照元へ戻る]

◆釣合平衡方程式

離散化数値解法で解析の対象とする問題は、左辺=右辺の形の方程式で記述されるが、この形の方程式を釣合平衡方程式と称する。常に左辺と右辺の値が等しくなるように定義されており、微小領域では解析対象のどの場所でもこの関係は満たされる。[参照元へ戻る]

◆並列計算機

単一ＣＰＵの計算機の計算能力を越えるために複数台のＣＰＵを用いて構成された計算機。現行のスーパーコンピュータはこのタイプである。並列計算機は大型の計算機に用いられている共有メモリ型並列計算機とＰＣクラスタに代表される分散メモリ型並列計算機に分類することができる。本ソフトウェアプラットフォームが対象としているのは後者であるが、大型の計算機でも分散メモリ的な使い方をサポートしていることが多く、その場合は大型の計算機でも使用できる。[参照元へ戻る]

◆連立方程式行列、マトリクスソルバー

離散化された連立一次方程式は、一般にAX=b　（ここでAは行列、X,bはベクター）の形で示される。Aは連立方程式行列（係数行列）、Xは未知数である解ベクトル、bは既知数である。「連立一次方程式を解く」ということはAとbが与えられた時にXを求めることであるが、これを行うプログラムがマトリクスソルバーである。数値解析ソフトウェアの計算性能の多くを占める部分であり、多種多様な手法が提案されている。[参照元へ戻る]

◆ソフトウェアテンプレート

プログラムの指定された箇所で指定された様式でサブルーチン（副プログラム）を呼び出したり、ユーザーが開発したサブルーチンをはめ込むことによって、問題解決を行うことが可能な構造を持つプログラムの雛型のこと。[参照元へ戻る]

◆ブラックボックス的使用

プログラムで用いられている解析手法、アルゴリズムの詳細が不明なまま、そのプログラムを使用すること。商用ソフトの大半はソースコード公開ではないため、ブラックボックス的使用となる。例えば「零による割り算による不具合が起きるのを避けるために、プログラム内で零の代わりに適当に小さな数値に置き換えて回避する処置を取っている場合、適当な数値解が出力されるために、入力データの不具合等、重要なミスを取り逃がす危険性がある。」また「プログラム内で、解析結果にスムージング等適当な後処理を施している場合、ブラックボックス的使用では解析結果の不具合を見逃す危険性がある。」一般にソフトウェア内部の詳細アルゴリズムが不明であると、解析上の不具合の原因究明が非常に困難である。[参照元へ戻る]

◆インハウス

商用のソフトウェアを購入して使用するのではなく、目的に合ったプログラムを自己の手で開発する事。[参照元へ戻る]

◆サブルーチンプログラム（subroutine call文）

プログラムに従った処理の中で同じ処理を何度も繰り返す場合に、その処理を何度も記述せず、別形式の副プログラムとして記述し、本プログラムから呼び出して用いることが行われるが、その呼び出し手続き。副プログラムをサブルーチンプログラムと呼び、本プログラムからの呼び出し手続きにCALLという命令が用いられるので、この手続き全体を称して「subroutine call」、本プログラム中のその部分を「subroutine call文」と呼ぶ。なお、サブルーチンとしては本プログラム中の繰り返し処理部分の他に、連立一次方程式の解法や乱数発生、補完・平滑化、フーリエ解析、数値微積分などの汎用に用られる定型処理部分を集めたものがあり、同じようにCALL文で呼び出して用いられる。[参照元へ戻る]

◆非対称行列

行列の各要素a_ijが対角線を対称軸として同じ値をとる（a_ij=a_ji）とき、この行列を対称行列と呼ぶ。それ以外の行列は非対称行列である。数値解析では、定常弾性問題、定常熱伝導問題等の線形問題については、連立一次方程式の係数行列が対称行列となるが、各種非線形問題等は、一般には非対称行列となる。[参照元へ戻る]

◆GMRES法、Bi-CGSTAB法、バンドマトリクス法

GMRES法、Bi-CGSTAB法、バンドマトリクス法はマトリクスソルバーの代表的な方法である。GMRES法、Bi-CGSTAB法は反復法と呼ばれる手法であり、近似値Xkを方程式へ入力して新たな近似値Xk+1を得る繰り返し計算を方程式全体の残差（b-AXk）が十分小さくなるまで行うことによって解を得る方法である。近似値Xkから新しい近似値Xk+1を得るアルゴリズムには様々なものがあり、それぞれに特徴を有するが、GMRES法は流体計算、Bi-CGSTAB法は構造計算に向いた手法である。
一方、バンドマトリクス法は直接法と呼ばれる解法の1つであり、基本的にガウスの消去法（掃き出し法）に基づく手法であり、反復法が不得手とする非線形が非常に強い問題に用いる。[参照元へ戻る]

◆MPI

MPI(Message Passing Interface)とは、 並列処理用のメッセージパッシングの規格である。 メッセージパッシングとは、メッセージと呼ばれる特定のデータ形式の受け渡しと、これらの一元的な管理に基づく通信手段の一つである。並列計算機の各ＣＰＵ間では数値計算の過程で多くのデータの交換が行われているが、その交換手順を定めたものがMPIである。多くの並列計算機に標準実装され、また、フリーウェアとしてmpich、LAM等のパッケージが入手可能である。本ソフトウェアプラットフォームはMPIのメッセージ交換手順に従って並列計算を進めていく。[参照元へ戻る]

◆METIS

ミネソタ大学が開発したグラフ分割用ライブラリ。フリーウェアとして入手可能である。要素-節点の結合情報をグラフとして認識し、それに基づいて領域の分割を行う。[参照元へ戻る]

◆離散化モデル

連続体である対象物を、小領域の集まりに離散化した物理モデル。離散化領域データ（要素、格子、セル等）と物性値、各種境界条件・荷重条件から構成される。[参照元へ戻る]

◆三次元弾性有限要素解析プログラム

三次元の弾性問題を解析するための定常線形有限要素解析プログラム。[参照元へ戻る]

◆変形および等価応力図

解析対象に荷重を課した結果生じた変形及び応力分布を示している。図において、色が赤の部分の応力が高く、青の部分の応力は低く表されている。[参照元へ戻る]

◆収束判定が10^-15

反復法における残差が10^-15以下の時、繰り返し計算が収束したと判断し、解を出力するという意味。
10^-15という値は大規模解析での収束判定条件としては非常に厳しい。[参照元へ戻る]

◆ＣＰＵtimeは１５５０秒

計算機が計算に要した実計算時間が１５５０秒であるという事。[参照元へ戻る]

◆並列化効率７０％以上

１台の計算機で実行した場合の所要時間をＴ1、ｎ台の並列計算機で実行した場合の時間をＴnとする。並列化効率は(T1/Tn)/nで定義される。並列化効率とは、並列化されたプログラムの性能を示す。この性能がよくないと、いたずらにプロセッサ数を増やしてもそれに応じた時間短縮効果を得ることはできない。[参照元へ戻る]

◆ドメイン・デコンポジション法

並列計算において、各ＣＰＵが担当する分割領域をまずそれぞれの分割領域の境界条件を仮定し、それぞれ独立に各ＣＰＵで並列計算し、分割領域間の境界面での物理量が収束するように境界面の境界条件を変更して、繰り返し計算を行う並列解析手法。大規模解析によって領域数が増えても容易に対応でき、データを他の領域に依存しないので、計算途中の通信コストを抑えることが可能である。[参照元へ戻る]

◆処理速度が20倍以上（32ノードにて70%以上の並列化効率）

並列化効率の定義式(T1/Tn)/nにおいて、T1=1 n=32と置くと、Tn=1/22.4である。ゆえに処理速度が20倍以上となる。[参照元へ戻る]