独立行政法人 産業技術総合研究所【理事長 野間口 有】(以下「産総研」という)エレクトロニクス研究部門【研究部門長 金丸 正剛】 量子凝縮物性グループ 柳澤 孝 研究グループ長らは、銅と酸素を主要な構成元素として高温で
超伝導を示す化合物のモデルについて、
電子の間に働く
クーロン力により超伝導が起こりうることを理論計算により示した。
クーロン力が電子を引きつける「のり」として働き、超伝導を引き起こすかどうかは、銅酸化物が高温で超伝導を示すことが発見されて以来、20年来の課題である。定説であるBCS理論によれば、通常の超伝導体では電子と原子振動との相互作用により超伝導が生じるので高い温度での超伝導は期待できないとされている。それに対し、もしクーロン力により超伝導が引き起こされるならば、より高い温度での超伝導が可能であると予想されている。この予想のようにクーロン力による超伝導が実現すれば、より高い温度での超伝導技術の幅広い応用が期待される。
今回、銅酸化物高温超伝導体の二次元モデルについて、量子モンテカルロ法を用いて大規模な理論計算によるシミュレーションを行ったところ、クーロン力が「のり」の役割を果たし超伝導を引き起こす可能性があることがわかった。
本研究成果は、日本物理学会の科学誌Journal of the Physical Society of Japanに発表された(Journal of the Physical Society of Japan 79 (2010) 063708)。
 |
|
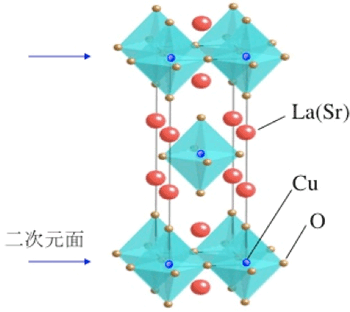
図1. 銅酸化物高温超伝導体La2-xSrxCuO4の結晶構造
(今回のシミュレーションは、矢印で示した面について行った)
|
超伝導状態では、電気抵抗がない。すなわち電力を損失しないで電流が流れるため、高温超伝導には様々な応用の可能性があり注目を集めている。エネルギー損失のない送電、リニアモーターカー、磁気共鳴画像法(MRI)など、より高い温度での超伝導の応用が期待されている。現在、超伝導状態への転移が起きる温度(臨界温度)の最高温度は常圧下で、およそ絶対温度135 K(およそ-138 ℃)である。理論的な側面から高温超伝導のメカニズムが明らかにされたならば、より高い臨界温度を得るための指針が得られ、材料科学、超伝導技術、デバイス応用に大きなインパクトを与えるものと期待されている。
産総研では、高温で超伝導を示す化合物の特性や温度、圧力、磁場などによる影響、超伝導メカニズムを明らかにするための研究を行っている。
銅酸化物からなる高温超伝導体は電子の間に働くクーロン力が大きく、強相関電子系と呼ばれ、実験面、理論面ともに、電子の状態を明らかにすることが簡単ではない。産総研では、高温超伝導体の性質、超伝導メカニズムを明らかにするために、量子モンテカルロ法などを使った理論計算の研究を進めている。今回、これらの計算手法を、クーロン力が働く超伝導体モデルに適用し超伝導状態の解析を行うこととした。
なお、本研究は、独立行政法人 科学技術振興機構 戦略的創造研究推進事業チーム研究(CREST)「超伝導新規応用のためのマルチスケール・マルチフィジクスシミュレーションの基盤構築」および独立行政法人 日本学術振興会 科学研究費補助金「量子モンテカルロ法および第一原理計算による2次元強相関系の研究」の一環として行われた。
定説であるBCS理論によると、通常の超伝導体では電子と原子振動との相互作用が「のり」となって電子対が形成され超伝導が起きているが、原子振動のエネルギーが小さいので高い温度での超伝導は期待できない。ところが、クーロン力により超伝導が引き起こされるならばクーロン力は大きなエネルギーをもつため、より高い温度での超伝導が期待できる。
図1に典型的な銅酸化物の高温超伝導体の結晶構造を示す。その物理的性質は、銅原子と酸素原子を含む面(図2)にある電子の状態によって決まると考えられている。この二次元面上の銅原子の電子に着目し、クーロン力を考えたモデルを考え、量子モンテカルロ法を使って超伝導状態の理論解析を行った。
 |
|
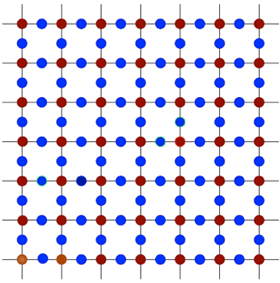
図2. 銅・酸素面の構造。茶色が銅原子、青が酸素原子を表す。
(図1の水平面を上から俯瞰した図に相当)
|
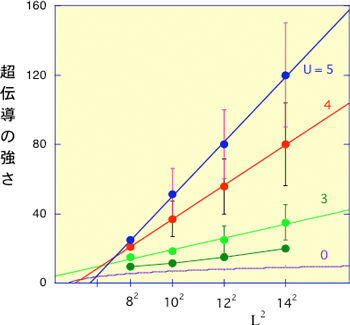
高温超伝導の二次元面のモデルに対して量子モンテカルロ法を用いた計算機シミュレーションを行ったところ、コスタリッツ・サウレス型の相転移として超伝導状態への相転移が起こりうることがわかった。モンテカルロ法とは、乱数を使って新しい配置を次々に生成していく方法であり、図3はそれによる配置の変化の一例を示している。一辺にL個の銅原子がある平面(図1の矢印で示される平面)でシミュレーションを行ったところ、超伝導の強さを表す量がLの2乗に比例し(図4)、超伝導が面全体に広がっていることを表している。コスタリッツ・サウレスの理論によると、これは超伝導相の存在を示唆している。すなわち、クーロン力が電子対の引力機構として働いていることを示している。
このシミュレーションの結果から、酸素と銅の結晶面をもつような化合物を合成することが、超伝導物質を得るための一つの指針と考えられる。また、クーロン力が大きくなると臨界温度も上がるものと予想される。
 |
|
図3. モンテカルロ法による計算の進行に伴う配置の変化の例。
ここでは、例えば、青が上向きスピン、赤が下向きスピンを表す。
|
 |
|
図4. 超伝導の強さを表す量のサイズ依存性。一辺にL個の銅原子がある平面の広がり(L2)に比例しており、電子対が結晶面全体に広がっていることを示している。Uはクーロン力の大きさを示し、クーロン力が強くなると超伝導状態が強くなることがわかる。
|
今回の計算は限られたパラメーターに対して行ったが、より多くのパラメーターを使ってより高い臨界温度の可能性を明らかにしたい。また、より高温で超伝導を含む新機能材料の探索のための指針を提供し、これらをもとにしたデバイスシステム設計などへの応用研究を進める。